Modele obliczeń i redukcja złożoności
Pokazana w pierwszej lekcji idea systemu iteracyjnego nie jest jedynym modelem obliczeń (abstrakcyjnym przedstawieniem idei obliczeń). Większy rozgłos zdobył model stworzony (dużo wcześniej) przez Alana Turinga, zwany od nazwiska twórcy „Maszyną Turinga”. Przystępny opis tego modelu znajdziesz na stronie: https://eduinf.waw.pl/inf/prg/003_mt/0001.php
Bardziej zbliżony do współczesnych komputerów jest model von Neumanna.
Należy zwrócić uwagę na trzy aspekty modeli obliczeń:
1) Tworzenie modeli obliczeń można powiązać z panującym w nauce dążeniem do poszukiwania prostych reguł objaśniających złożone procesy – w tym procesy obliczeń (Redukcjonizm, Logicyzm). Z jednej strony te prace zbudowały fundament informatyki, a z drugiej – niestety – przyczyniły się do upowszechnienia współczesnej formy materializmu, opartego o (błędne) przekonanie o triumfie redukcjonizmu i determinizmu.
2) Teoretyczne znaczenie modeli obliczeń wiąże się z szukaniem miary złożoności. Szacowanie złożoności obliczeń jest jedną z dziedzin najważniejszych dla rozwoju cywilizacji (dzięki niej mamy nowoczesną kryptografię). Możliwość zredukowania różnych procesów obliczeń do wspólnego modelu pozwala na porównywanie ich złożoności, ale także – do ustanowienia miar złożoności. Na przykład – ile operacji musi wykonać maszyna Turinga, by zakończyć obliczenie (zobacz też: https://logic.edu.pl/computing/12-zlozonosc). Przy okazji sformalizowano problem stopu: obliczenie jest wykonalne, jeśli maszyna je wykonująca kiedykolwiek się zatrzyma.
3) W latach 40-tych XX wieku zauważono, że modele obliczeń mogą zostać użyte do zaprojektowania rzeczywiście działających maszyn. Przyczyniły się do tego między innymi prace zespołu (z bardzo dużym udziałem polskich matematyków) zajmującego się łamaniem niemieckich szyfrów Enigma.
W tych pracach krystalizuje się dwie podstawowe idee:
1. Dokonywanie zmian małymi porcjami w takt zegara. Jeśli automat ma zsumować dwie liczby, to może to zrobić w jednym kroku, albo wielu kolejnych – za każdym razem sumując cyfry na kolejnych pozycjach (zapis pozycyjny).
2. Instrukcje działania automatu mogą być pamiętane tak jak przetwarzane dane. Kolejne instrukcje (polecenia działania w kolejnych krokach) są pamiętane tak jak dane. Wydzielona zostaje część maszyny zwana procesorem, która pobiera dane i instrukcje z pamięci i wykonuje instrukcje na pobranych danych. Wiąże się to z przekonaniem, że złożone instrukcje daje się zredukować do skończonej listy prostych instrukcji (instrukcji procesora).
Procesor
Procesor musi więc posiadać także komórki pamięci, do których będzie pobierał dane i instrukcje do przetwarzania. Takie komórki pamięci w procesorze nazywa się rejestrami. Poniższy rysunek (szerszy opis na stronie https://wiki.otwartaedukacja.pl/index.php?title=Procesor_i_j%C4%99zyk_maszynowy_-_wprowadzenie#Projektujemy_procesor) przedstawia procesor z czterema rejestrami:
-
licznik – zawiera numer komórki pamięci (adres) z której są pobierane dane i instrukcje
-
instrukcja – pobierana instrukcja
-
parametr – parametr dla instrukcji
-
akumulator – wynik instrukcji, który może być parametrem dla kolejnej instrukcji
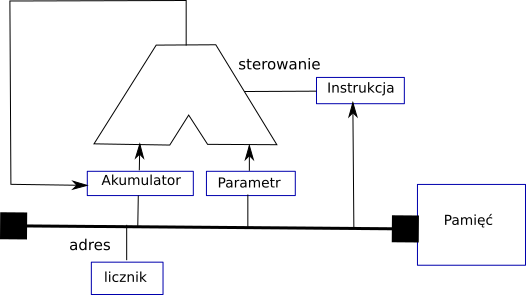
Pobranie kodu instrukcji lub parametru zwiększa licznik o 1.
Oprócz tego muszą być dostępne instrukcje zmieniające licznik na wartość pamiętaną w parametrze (przepisz wartość parametru do licznika).
Lista instrukcji zaproponowana do powyższego procesora:
|
nazwa |
kod |
parametr |
opis |
|
POBIERZ |
1 |
adres danej |
przepisuje zawartość wskazanej komórki pamięci do akumulatora |
|
APOBIERZ |
2 |
adres pamięci |
przepisz do akumulatora zawartość komórki o adresie wskazanym przez adres pamięci |
|
WPISZ |
3 |
adres danej |
zapisuje zawartość akumulatora do wskazanej komórki pamięci |
|
DODAJ |
4 |
adres danej |
dodaje zawartość wskazanej komórki do zawartości akumulatora |
|
USTAW |
5 |
liczba |
ustaw zawartość akumulatora na liczba |
|
SKOCZ_DO |
6 |
adres |
wpisz adres do licznika |
|
ZERO |
7 |
adres |
gdy akumulator zawiera zero, wpisz adres do licznika |
|
STOP |
0 |
0 |
zatrzymaj |
Przykładowy program napisany przy użyciu tych instrukcji:
USTAW LICZBY
WPISZ ADRES
USTAW 0
WPISZ WYNIK
A: POBIERZ ILOSC
ZERO K
DODAJ -1
WPISZ ILOSC
APOBIERZ ADRES
DODAJ WYNIK
WPISZ WYNIK
POBIERZ ADRES
DODAJ 1
WPISZ ADRES
SKOCZ_DO A
K: STOP
Program ten sumuje liczby zapamiętane w pamięci. Poza kodami instrukcji w powyższym zapisie pojawiły się symbole oznaczające adresy pamięci.
LICZBY – miejsce pamiętania (adres) liczb do zsumowania
ADRES – adres aktualnie sumowanej liczby
WYNIK – adres wyniku
ILOSC – adres komórki pamięci w której zapamiętano
A – adres pamiętania instrukcji programu „POBIERZ ILOSC”
K – adres instrukcji programu STOP
Wartość K i A możemy ustalić dopiero po zamianie powyższego symbolicznego zapisu na kody i wskazaniu w którym miejscu pamięci będzie ten program zapisany.
Taki symboliczny zapis zapis programu nazywa się kodem asemblera. Asemblerem nazywamy też program przekładający ten zapis na kody maszyny.
Porównaj to z architekturą jednego z pierwszych mikroprocesorów: https://pl.wikipedia.org/wiki/Intel_8080
Opis Asemblera dla tego mikroprocesora znajdziesz tu: https://pl.wikibooks.org/wiki/Asembler_x86